Minesweeper has always been a fun little game that you can throw up in your free time that still requires a minimum amount of logical problem solving in order to win. During our morning meeting for Lab Day the topic of Minesweeper was brought up so I decided to make an algorithm that tries to play the perfect game of Minesweeper. For starters I needed a basic javascript minesweeper game with all the square data stored so I didn’t have to create an interface with the classic game. I found a simple one on github that ended up being perfect.

Then it was time to start to implement the logic. First step was very simply having a square randomly selected to start the game. Next was to start implementing the most common logical cases. The first logical case was one that any player starting out in minesweeper could identify and is as follows…
- If a tile has the same amount of hidden squares around it as unflagged bombs remaining around it, then all the hidden squares are bombs.
This case is easily illustrated by an example like this. The algorithm can now understand which squares are bombs for sure.
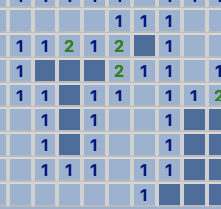
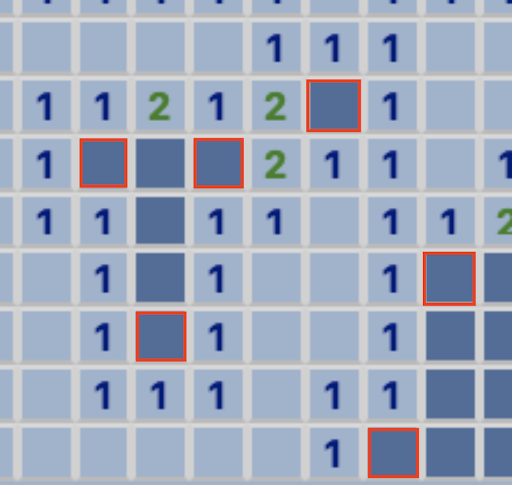
Moving on from here, there is an easy way to clean up a lot of the mess that is left over after we have dealt with marking all these bombs. That leads us to our next logical case.
- If a tile has the same amount of flags around it as the number on the square, then all remaining hidden tiles around it are not bombs.
So essentially this is to make progress on the board by clicking on squares that are certainly not bombs and therefore receiving more information. For example, we know these green squares are safe and can be selected.


With just these two steps in place the algorithm is at about a 70-80% winrate. Which is good but it can be better. If the board can’t make any more progress it will randomly select one from the tiles left. This is not a good system and frequently results in a loss. Therefore one more search is in order before the algorithm chooses a random tile.

With the current two steps in place, no progress can be made here. But logically it is very possible. If you look at the 3, we know there are two unflagged squares touching it. We know from the two flags already touching it. With this we know that between those last two unflagged squares, there must be exactly one bomb. Therefore these two tiles are now linked and the algorithm will run again using this new information. The outcome will be one tile being selected and the other flagged.

This gets the winrate to about 80%. But there are too many logical cases to program in one day. The most interesting observation to come out of this project was the realization that almost every game of minesweeper is almost completely decided by chance. What I mean by that is, even if a human or a computer plays the game 100% perfectly and uses every possible logical scenario, more often than not it will eventually be forced to guess. On a board thousands of tiles wide, if the last tile you had to pick was a 50/50 random chance, then you never really had higher than a 50/50 chance to begin with. After a little research I found a post where someone had done the math stating that if board size and number of bombs scaled at the same ratio, once you get into the higher thousands in board size, the winrate of a perfect game would never be higher than 5% just due to the sheer amount of guessing required in such a large board. Anyway, here’s the finished product!